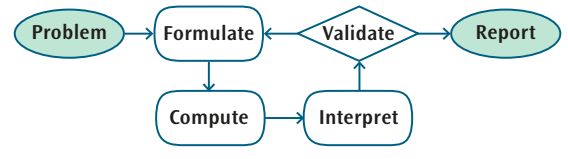
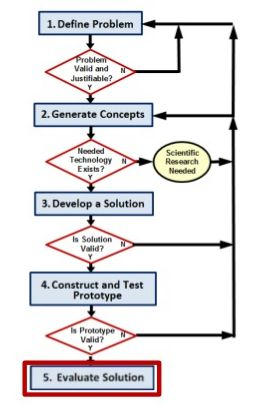
Functional Design Through Algebra
Title:Functional Design Through Algebra (UCCI)
Length of Course:Full Year (2 semesters; 3 trimesters; 4 quarters)
Subject Area – Discipline: Mathematics (“c”) - Algebra 1
CTE Sector:Engineering and Architecture
CTE Pathway: Engineering Design Grade/Level(s):9-12
Course Overview:
In this engaging, hands-on course, students will discover the power of mathematical modeling with algebraic functions. Through a variety of Engineering Design projects, students must utilize functions to optimize the outcome of each challenge. Students will see parallels between the mathematical modeling cycle (top image) and the engineering design process (bottom image) in each unit. Students will design parachutes, bungee jumps, boats, balloon rockets, a variety of water fountains, and, as a capstone project, a thermally resistant beverage container along with product proposal and pitch. Students will document calculations, graphical relationships, sketches of prototypes and final designs in an engineering notebook that includes summaries of each project and ideas for future redesigns. By building understanding of functions, graphs, equations, and algebraic relationships, students will see how mathematical understanding can verify optimal performance and design in a variety of applications.
Course Content:
Unit 1-Introduction to Engineeering Design Process
Students are introduced to the Engineering Design cycle by learning its five phases and then experiencing it firsthand through 3 different situations: designing a parachute, creating and calibrating a spring scale, and calculating the appropriate distance for a bungee jump. Through this unit, students must 1) Define a problem, 2) Plan and build a prototype, 3) Test the prototype, 4) Measure results, and 5) Analyze data to propose improvements. Students will carefully design ways to gather and record data in all three assignments in this unit, and will analyze the data to learn key mathematical relationships involving surface area, Hooke’s Law, linear equations (slope/intercept form), graphical analysis, and experimental research.
Unit 1 - Key Assignments
Lab Assignment 1: Build a Parachute: Students are given a set of materials and asked to make a parachute apparatus that will keep a paper clip payload aloft for the longest possible time, while also attempting to land within a specified target area. Given only plastic sandwich bags, string, tape, and an index card, students design and assemble their parachute apparatus to accomplish two objectives. The first performance metric is the measured length of time the apparatus remains in the air when dropped from a specified height, while the second metric is the measured landing distance from the plumb line point located on the landing surface. Students follow the engineering design process by first drawing up initial plans of their prototypes in their engineering notebooks, which are then reviewed and approved before getting the materials.
Once assembled, students drop the apparatus and record the hang time, as well as the distance between the landing point and the target point. Students then measure the surface area and make a scatter plot of surface area versus hang time, and surface area versus target accuracy (distance from target point). Using the data, students investigate the relationship between the input variables (surface area) and the output variables (hang time and horizontal distance traveled from target landing point). Students identify the key physical factors affecting output, while recognizing the potential for an optimal performance. They use their quantitative analysis and observational data to justify any redesign to their projects. They will redesign and test to see if mathematical analysis improved their projects.
Lab Assignment 2- Build a Balance: To develop understanding of elastic materials and linear equations, student teams will compete to design, build, and test the most accurate “mass weighing device” that could be used to determine the weight of household objects. Through the research and testing process, students will discover the linear nature of springs through Hooke’s Law.
Students will begin by analyzing the relationship between an input force (weight) and the resulting extension of a given elastic material. By graphing their data and using a best fit analysis, students will establish a linear relationship between the independent variable (force/weight) and the dependent variable (stretch length) and interpret the significance of the line’s slope. Teams then construct the device and test it for accuracy by weighing a variety of objects and performing error analysis compared to an electronic scale. Students will understand the nature of linear functions, their slope through testing various inputs, and observing how the output changes. Teams will finally be given a set of three unknown masses to weigh, and students will share their results as a class. Students will analyze the class data to determine the standard deviation, and percent error against the accepted weight values.
(Optional) Lab Assignment 3- Build a Bungee Jump: [Note: This could be an extension/optional assignment based upon students’ developing facility with math and engineering.] Acting as engineering consultants, students are hired by an outdoor adventure company to design a safe and economical bungee jump that meets the company’s specifications. Armed with their newfound knowledge of both functions and the behavior of elastic springs, students then begin dynamic testing of various bungee jumps of various weight ranges specified by the adventure company, but for a specific “jump length” to maximize exhilaration. By plotting the data as a class, students will find the acceptable domains of the independent variable (weight ranges of potential customers) when other variables are fixed (height, elasticity of bungee cord). Students will identify the linear relationship between falling distance, and the length of the cord as well as the significance of the slope’s dependence on the falling weight. After analyzing the data, students share their design details with the company in a written report that specifies the optimal cord length range as a function of the customer’s weight.
Unit 2 - Archimedes’ Challenge- Build a Boat
Students design and construct rectangular paper boats that must keep various objects afloat. Students first identify the input parameters of the design specifications and then calculate dimensions for the initial designs of their vessel. Once the students have created design sketches in their engineering notebooks, they will then be given the materials to create prototypes for testing. For each iteration, students measure and record data on surface area and volume, which is then shared in a data repository so that the class can track performance data. The metric used for this design challenge will be to create the boat with the least surface area that can successfully keep the object above water. Once the prototype boats have been created, students will test their boats. After the initial test, students will then return to the design phase to revisit their initial ideas and make modifications. Performance information will be shared and the class will analyze mathematical relationships like surface area to volume, length and width ratios, and any other relevant data patterns. Using insight from these relationships, students will be able to incorporate the analysis into the redesign process for subsequent boats.
Unit 2 - Key Assignments
Lab Assignment 1: Build a Cardboard Boat: Students are given cardboard materials and asked to design and construct a rectangular boat that must float when carrying a unique payload: their phone. Students first cut out squares of varying sizes from the four corners of the material, and must decide how high to make the boat’s walls. Students determine the buoyant forces for various boat designs by altering the volume of the boat (a rectangular solid). To maximize volume (which determines buoyancy), students must set up and solve a quadratic equation whose solutions reveal what size squares to cut out from each corner of the cardboard rectangle before folding the sides up to construct the boat. Students will record all equations and design calculations in their engineering notebooks, along with scale drawings of each prototype design. Students will cite mathematical evidence in a summary statement that cites the technical reasons for their final design.
Lab Assignment 2: Build a Bigger Boat: Students now must design and construct a new boat that must float two phones. Doubling the payload forces students to again optimize their materials by using equations from Assignment #1 to find new solutions for a boat requiring twice the buoyant forces. Students will be asked to consider how they could use the optimization function to find the dimensions of any new boat that must hold a specific weight. Students will hypothesize how the function parameters must change in order to scale for a different input weight, then must solve a second quadratic equation to see how the dimensions must change to double the buoyancy of this new boat. Students record all calculations and new design drawings in their engineering notebooks.
Lab Assignment 3: Build a Full Size Boat: Students must utilize their algebraic function to make one more design, this time the boat is made from cardboard and must hold…a student! Students must consider how scaling a boat affects each dimension, each property of the boat, (surface area, volume), and must determine if their design can hold a student’s weight. Using the math skills learned from the first two assignments, students will design this third boat for the lightest weighing student in their group, then must float the boat for the longest amount of time in a culminating competition against the entire class. Upon completion of the competition, all students write a paragraph in their engineering notebook that summarizes the key mathematical concepts learned in the unit, including: the importance of mathematical modeling, how to optimize a design by solving quadratic equations, and how increasing the scale of a prototype affects the design parameters for an increased payload.
Unit 3 - Quadratics in The Garden - Designing A Fountain
Students will design a water fountain by writing multiple quadratic equations and graphing them to represent decorative parabolic streams of water. Students will write and graph quadratic equations in both Vertex and Standard Form. The various streams of water will originate from different heights and have different trajectories, requiring students to work in both the first and second quadrants of the cartesian coordinate system. Students must calculate the x and y coordinates of each apex, and each starting and ending point of the stream of water, along with its axis of symmetry, to ensure a decorative and aesthetically pleasing fountain. Once the design is completed, the students must calculate which types of pumps they will need to purchase for each stream of water by analyzing the required pressure and orifice size to ensure the required velocity to ensure the streams follow their designed trajectory.
Unit 3 - Key Assignments
Assignment 1: Graphing Parabolas through x-intercepts:
Students graph quadratics by graphing the x-intercepts first after factoring a simple quadratic equation that fits their first stream of water for the fountain. Students must identify and draw the axis of symmetry by finding the midpoint of the x-intercepts and then locate the vertex of the parabola that will be the stream of water’s trajectory. This method allows students to make connections between the x-intercepts and the parabola. Students draw a sketch of the parabola along with all calculations into their Engineering Notebooks to clarify that the x-intercepts determine the beginning and ending points of each stream of water. Students will also label the x and y coordinates of the vertex, and explain in a short summary how they located each key point of the parabola and describe its significance. Finally, students will plot their equations using an electronic graphing tool (Desmos, Plotly, graphing calculator), verify whether or not their handwritten graphs are accurate, and cite any domain and range restrictions for their designed fountains.
Assignment 2: Graphing through vertex form:
Students will now write equations for two more streams of water in the fountain, but they will find the key points from different information and through a different method of mathematical analysis. Students will be given the apex of two opposing (but symmetrical) streams of water, and must use the vertex form of quadratic equations to find the x-intercepts. Once the quadratic equation that describes the parabolic trajectory is written, students will then convert it from Vertex Form to Standard Form.
This will allow students make connections between the vertex and the parabola. Students will accurately draw each parabola, write the equation in both forms, and describe in their engineering notebooks how to use both Vertex Form and how to convert it to Standard Form for parabolas. Students will also write a short summary of how to precisely determine the apex and x-intercepts, and what the significance of each point is for each stream of water.
Assignment 3: Exploring the leading coefficient:
Students will use online graphing software to explore and understand the impact of various leading coefficients by graphing different quadratic equations in different forms. At first, students will be given x-intercepts, and must write the equation in standard form, then adjust the height of the parabola by adjusting the leading coefficient (scalar multiple). Second, when given the vertex, students will change the leading coefficient to observe the effect on the x-intercepts. Students again will write a summary that explains how the leading coefficient affects the shape of each stream of water. Using this new understanding, students are asked to add two more streams of water that would add to the aesthetic beauty of the existing streams of water (from Assignments 1 and 2). Students must use various “a values”for their new parabolas to show understanding, and must sketch the trajectories in their engineering notebooks along with the appropriate quadratic equations for each new stream of water.
Graphing Software:
Math/Lab Assignment 4: Design of Water Fountain
Starting from scratch, students are challenged to create an entirely new water fountain of their own design. Using what they learned from the first three assignments, they must graph and write the equation (in both Standard and Vertex Form) for each stream of water. Students must include appropriate domains and ranges for each equation written. Once the design is complete, the instructor will help students with kinematic equations from physics to find the required velocity to make each fountain precisely match the designed trajectory. Once provided with this velocity, students then research various water pumps by finding the required pressure rating (in psi, or pounds per square inch) for each pump and then identify available pumps from various suppliers (ex. Granger, Ingersoll/Rand, etc.). Students will write a detailed cost proposal that includes specific pump models, specifications, and velocities, and must support their proposal with mathematical evidence justifying the cost of each pump. If budgets allow for it, teachers have the option of actually ordering enough pumps to assemble and test the designed fountains and see if the calculated x-intercepts, apexes, and axes of symmetry match the design.
Extension Assignment - CAD Design of Water Fountain
Using a freely available CAD software program like Sketch-Up or TinkerCAD, students will design the fountain as a virtual 3D object, using the previous calculations to specify the dimensions of the design.
SketchUp(Browser Version)
TinkerCAD( Browser-based)
https://www.tinkercad.com/
Unit 4 - Balloon Rockets
Students will follow the engineering design process to design a transport vehicle that will travel an unknown distance powered by an inflated balloon. Built from simple materials, the student-made vehicles will race across the room while suspended from two fishing lines. Students will implement and diagram the Universal Systems Model of problem solving to develop their vehicles. Once built, students will gather test data to explore mathematical relationships and patterns between the balloon’s volume, radius, and distance traveled. Students will plot multiple data points for a wide variety of balloon volumes to develop a graph that will allow them to use the relevant independent variable (balloon size) to predict the value of the dependent variable (distance traveled). Students will then be given a predetermined distance, and must use their established function to inflate their balloon accordingly to make their vehicle precisely travel the target distance.
Unit 4 - Key Assignments
Assignment 1: Problem Definition and Idea Generation
Students first draw up plans for their prototypes, which must be approved before getting the materials. Students will create thumbnail sketches, a rough sketch, and a final scaled drawing using measurement of inches. All sketches, drawings, and design notes will be done in students’ engineering notebooks.
Lab Assignment 2: Build The Design
Students will build their design using household materials (paper towel rolls, straws, string, toothpicks, cardboard, etc.). Each student will get a balloon of the same size and color. Students are to build their prototype to carry an object of their choice (lego figurine, washer, weight, etc.). The object must be able to be set on the vehicle without being attached in any way. Students will be given an initial minimum distance their vehicle must travel, as well as a maximum balloon diameter. Students continue to use their engineering notebooks to record data, sketches and such.
Lab Assignment 3: Test and Collect and Analyze
Students will use the mathematical model to figure out a predictable output for their balloon transport vehicle. Using the data, students determine what relationship there is between the variables and write a function equation using proper function notation. They will retest their designs by changing fuel input (balloon inflation) and corresponding mass of vehicle until they find a formula that will allow them to plot data points to accurately predict an outcome. Students will document their design drawings, their test results, and their reflections on the process into their engineering notebooks to record the relationship between balloon volume and distance traveled. On test day they should be able to use their data points based on previous investigation, that will allow them to know how much fuel they will need to reach the unknown distance.
Lab Assignment 4: Enrichment Activity-Optimize Fuel Usage
Performance information will be shared and the students will analyze possible patterns in the data. Students will incorporate the analysis into the redesign process for subsequent redesigns of their vehicles. After students reach the unknown distance on test day, they now must reach that distance using the least amount of fuel as possible. They must optimize fuel usage to determine the most efficient balloon transport vehicle. They will redesign and test to see if mathematical analysis improved their projects.
Unit 5 - Build A Better Bottle
In this unit, students will investigate the behavior of exponential functions while designing a product whose behavior models exponential decay through heat loss. Students will employ the engineering design process to conceive and create an insulated coffee cup/bottle that is constrained by several inputs: size, material costs, safety, and thermal properties. The project begins by defining the needs of the customer and the appropriate design parameters and limitations. Students will then research Newton’s Law of Cooling to better understand how an exponential decay function describes the performance of any device that is designed to retain heat.
Students will then explore the container’s behavior by altering different initial conditions and then using temperature sensors to gather and record data for multiple trials. By graphing this data, students will develop the shape of the cooling curve, and will use graphing tools to match the mathematical function (exponential) to their data. Students then engage in the design process to investigate problem parameters by researching material thermal resistances and material costs. Students create initial design drafts and calculate the material costs for constructing their product.
They then either use a CAD program (or traditional drafting techniques) to finalize their designs, while also calculating the thermal transfer parameters of their design. The students can then use these input parameters in the exponential model to determine the cooling rate for different liquids at different initial temperatures. Finally students create a proposal that includes the efficiency of their design as well as the calculated material cost. These proposals are presented as ideas to a “product manager” who assesses the manufacturability, cost and performance of the proposed products.
AutoDesk Fusion 360( PC/Mac)
http://www.autodesk.com/products/fusion-360/students-teachers-educators
http://www.autodesk.com/products/fusion-360/learn-training-tutorials
Unit 5 - Key Assignments
Lab Assignment 1:Measure cooling rates: Students use temperature sensors or thermometers to measure the cooling rates of a fluid of fixed volume in a coffee cup/water bottle. Students graph the data and then use a graph matching tool (LoggerPro, Excel, Plotly, etc.) to deduce the appropriate type of mathematical function. After sharing data with the entire class, students discuss the similarities and differences between quadratic functions and the behavior of the cooling function. Exponential functions are then introduced with the basic exponential function ( y = ax ), and students are given multiple examples of both growth and decay, along with numerous applications where these situations apply to physical phenomena.
Students are then given the specific mathematical structure of the cooling function:
T (t) = Ae−kt + TA
where TA= ambient temperature in the room, T(t)= temperature of liquid, A= initial temprature difference, k= cooling constant
Students analyze how the different coefficients (A, TA, -k) change the position and curvature of the exponential function. Other exponentia ls are also investigated in order to establish a common pattern. The goal of this assignment is to help guide the students towards an analytical tool for determining a performance function for their product.
Students record data gathered and discussion notes in their engineering notebooks in preparation for the culminating assignment.
Lab Assignment 2: Research Thermal Resistance and Thermal Qualities of Materials
Students research the physical parameters that actually affect the cooling function. This leads then to a discussion and further research into thermal properties of materials. Further investigations are designed to strengthen student understanding of how surface area, thermal resistivity, and thickness change the curvature of the cooling function. Student groups investigate the cooling rate of a known liquid through different containers with different surface areas, different thicknesses and different materials. Students will collectively produce a data report and analysis of the experimental input’s effect on cooling.
Lab Assignment 3: Design A Better Liquid Holder
Students are now given the design challenge parameters for designing a better liquid holder. The design requirements outline specific design parameters such as the size specifications of the product (must fit in a standard size cup holder), the function of the container (must have removeable lid and handle), and the cost range of the product. To better understand the consumer sales perspective of designing products, student designers will survey other students to get customer input on size, shape, and feel of various beverage containers. Once designers have enough responses to ensure statistical significance, they must then compile the data using a scatter plot or other graphical display to demonstrate understanding of customer preferences, so that any functionally-driven design decisions also consider the marketability of the product.
Students then produce design drawings of their product, including material choice and construction design. Once their designs are completed, students must justify the design parameters using mathematical evidence from their explorations of Newton’s Law of Cooling equation. All reflections, calculations, and design sketches are all entered in their engineering notebooks.
Extension Assignment: Model and Predict Product Performance
Using a software thermal analysis tool (Fusion360, etc), students can model the performance of their product based on the design they have proposed. Students generate a thermal analysis report and performance prediction based on material cost and design specs.
AutoDesk Fusion 360( PC/Mac)
http://www.autodesk.com/products/fusion-360/students-teachers-educators
http://www.autodesk.com/products/fusion-360/learn-training-tutorials
OnShape( Browser-based)
https://www.onshape.com/
OPTIONAL
Unit 6 - Design a “FUNctional” Graphical User Interface App
To provide students with an opportunity to use and apply their learning from the year in a new engineering context, students review the functional models covered throughout the course by designing and writing the code for graphical user interfaces, (“apps”) that simulate calculators for each of the mathematical representations or engineering equations covered in the course. The calculator accepts user input for the functional parameters of the problem, and generates the output for each functional model. By writing the computer code that processes the inputs to deliver the correct output, students must thoroughly understand the equations, possible inputs (including appropriate domains for independent variables), and must verify the outputs are flawlessly correct.
Unit 6 - Key Assignments
Assignment 1:
Students have been hired to design a calculator app which simulates different mathematical functions related to the engineering principles studied in the course. Students identify the parameters that each method definition should accept from the user by reviewing the parameters found in each of the three functional representations, and should define what each parameter will represent for the real-world model. The teacher should check that students generate the following functions and parameters:
For each of the three models or apps, students create a “Know/Need to Know” list for the app, which will inform their design decisions. Students write a formal proposal for each app they will design, and a timeline for the project.
Assignment 2: Design GUI: Once students have written the “interface” for the apps, they design each graphical screen which the user will interact with. Students define the screen or frame size according to their desired platform (Android, iPhone, website, etc.) and the typical “consumer” who will use each application, by researching and collecting data on their consumers, and using that data to inform the design decisions they make for the overall layout, colors, text fields, and buttons on the screen.
Students create a Google Form and/or survey for their target audience, with directed questions that will inform the design decisions for the graphical components on their app. Based on their ideal “consumer,” students must determine the questions and information needed for adequate feedback and informed decisions, and must then market the survey to the typical “consumer” within their community.
After gathering market data, students design and color their screen on graph paper, or using a computer application, then present a design proposal to the class for evaluation. After reaching a final design decision, students must identify the x and y coordinates, and dimensions needed, to properly place each component, then write the code for generating the graphical design.
Course Materials
Algebra Textbook: (use approved district math book)
Supplementary Text: Design Engineering Textbook (district approved)
Length of Course:Full Year (2 semesters; 3 trimesters; 4 quarters)
Subject Area – Discipline: Mathematics (“c”) - Algebra 1
CTE Sector:Engineering and Architecture
CTE Pathway: Engineering Design Grade/Level(s):9-12
Course Overview:
In this engaging, hands-on course, students will discover the power of mathematical modeling with algebraic functions. Through a variety of Engineering Design projects, students must utilize functions to optimize the outcome of each challenge. Students will see parallels between the mathematical modeling cycle (top image) and the engineering design process (bottom image) in each unit. Students will design parachutes, bungee jumps, boats, balloon rockets, a variety of water fountains, and, as a capstone project, a thermally resistant beverage container along with product proposal and pitch. Students will document calculations, graphical relationships, sketches of prototypes and final designs in an engineering notebook that includes summaries of each project and ideas for future redesigns. By building understanding of functions, graphs, equations, and algebraic relationships, students will see how mathematical understanding can verify optimal performance and design in a variety of applications.
Course Content:
Unit 1-Introduction to Engineeering Design Process
Students are introduced to the Engineering Design cycle by learning its five phases and then experiencing it firsthand through 3 different situations: designing a parachute, creating and calibrating a spring scale, and calculating the appropriate distance for a bungee jump. Through this unit, students must 1) Define a problem, 2) Plan and build a prototype, 3) Test the prototype, 4) Measure results, and 5) Analyze data to propose improvements. Students will carefully design ways to gather and record data in all three assignments in this unit, and will analyze the data to learn key mathematical relationships involving surface area, Hooke’s Law, linear equations (slope/intercept form), graphical analysis, and experimental research.
Unit 1 - Key Assignments
Lab Assignment 1: Build a Parachute: Students are given a set of materials and asked to make a parachute apparatus that will keep a paper clip payload aloft for the longest possible time, while also attempting to land within a specified target area. Given only plastic sandwich bags, string, tape, and an index card, students design and assemble their parachute apparatus to accomplish two objectives. The first performance metric is the measured length of time the apparatus remains in the air when dropped from a specified height, while the second metric is the measured landing distance from the plumb line point located on the landing surface. Students follow the engineering design process by first drawing up initial plans of their prototypes in their engineering notebooks, which are then reviewed and approved before getting the materials.
Once assembled, students drop the apparatus and record the hang time, as well as the distance between the landing point and the target point. Students then measure the surface area and make a scatter plot of surface area versus hang time, and surface area versus target accuracy (distance from target point). Using the data, students investigate the relationship between the input variables (surface area) and the output variables (hang time and horizontal distance traveled from target landing point). Students identify the key physical factors affecting output, while recognizing the potential for an optimal performance. They use their quantitative analysis and observational data to justify any redesign to their projects. They will redesign and test to see if mathematical analysis improved their projects.
Lab Assignment 2- Build a Balance: To develop understanding of elastic materials and linear equations, student teams will compete to design, build, and test the most accurate “mass weighing device” that could be used to determine the weight of household objects. Through the research and testing process, students will discover the linear nature of springs through Hooke’s Law.
Students will begin by analyzing the relationship between an input force (weight) and the resulting extension of a given elastic material. By graphing their data and using a best fit analysis, students will establish a linear relationship between the independent variable (force/weight) and the dependent variable (stretch length) and interpret the significance of the line’s slope. Teams then construct the device and test it for accuracy by weighing a variety of objects and performing error analysis compared to an electronic scale. Students will understand the nature of linear functions, their slope through testing various inputs, and observing how the output changes. Teams will finally be given a set of three unknown masses to weigh, and students will share their results as a class. Students will analyze the class data to determine the standard deviation, and percent error against the accepted weight values.
(Optional) Lab Assignment 3- Build a Bungee Jump: [Note: This could be an extension/optional assignment based upon students’ developing facility with math and engineering.] Acting as engineering consultants, students are hired by an outdoor adventure company to design a safe and economical bungee jump that meets the company’s specifications. Armed with their newfound knowledge of both functions and the behavior of elastic springs, students then begin dynamic testing of various bungee jumps of various weight ranges specified by the adventure company, but for a specific “jump length” to maximize exhilaration. By plotting the data as a class, students will find the acceptable domains of the independent variable (weight ranges of potential customers) when other variables are fixed (height, elasticity of bungee cord). Students will identify the linear relationship between falling distance, and the length of the cord as well as the significance of the slope’s dependence on the falling weight. After analyzing the data, students share their design details with the company in a written report that specifies the optimal cord length range as a function of the customer’s weight.
Unit 2 - Archimedes’ Challenge- Build a Boat
Students design and construct rectangular paper boats that must keep various objects afloat. Students first identify the input parameters of the design specifications and then calculate dimensions for the initial designs of their vessel. Once the students have created design sketches in their engineering notebooks, they will then be given the materials to create prototypes for testing. For each iteration, students measure and record data on surface area and volume, which is then shared in a data repository so that the class can track performance data. The metric used for this design challenge will be to create the boat with the least surface area that can successfully keep the object above water. Once the prototype boats have been created, students will test their boats. After the initial test, students will then return to the design phase to revisit their initial ideas and make modifications. Performance information will be shared and the class will analyze mathematical relationships like surface area to volume, length and width ratios, and any other relevant data patterns. Using insight from these relationships, students will be able to incorporate the analysis into the redesign process for subsequent boats.
Unit 2 - Key Assignments
Lab Assignment 1: Build a Cardboard Boat: Students are given cardboard materials and asked to design and construct a rectangular boat that must float when carrying a unique payload: their phone. Students first cut out squares of varying sizes from the four corners of the material, and must decide how high to make the boat’s walls. Students determine the buoyant forces for various boat designs by altering the volume of the boat (a rectangular solid). To maximize volume (which determines buoyancy), students must set up and solve a quadratic equation whose solutions reveal what size squares to cut out from each corner of the cardboard rectangle before folding the sides up to construct the boat. Students will record all equations and design calculations in their engineering notebooks, along with scale drawings of each prototype design. Students will cite mathematical evidence in a summary statement that cites the technical reasons for their final design.
Lab Assignment 2: Build a Bigger Boat: Students now must design and construct a new boat that must float two phones. Doubling the payload forces students to again optimize their materials by using equations from Assignment #1 to find new solutions for a boat requiring twice the buoyant forces. Students will be asked to consider how they could use the optimization function to find the dimensions of any new boat that must hold a specific weight. Students will hypothesize how the function parameters must change in order to scale for a different input weight, then must solve a second quadratic equation to see how the dimensions must change to double the buoyancy of this new boat. Students record all calculations and new design drawings in their engineering notebooks.
Lab Assignment 3: Build a Full Size Boat: Students must utilize their algebraic function to make one more design, this time the boat is made from cardboard and must hold…a student! Students must consider how scaling a boat affects each dimension, each property of the boat, (surface area, volume), and must determine if their design can hold a student’s weight. Using the math skills learned from the first two assignments, students will design this third boat for the lightest weighing student in their group, then must float the boat for the longest amount of time in a culminating competition against the entire class. Upon completion of the competition, all students write a paragraph in their engineering notebook that summarizes the key mathematical concepts learned in the unit, including: the importance of mathematical modeling, how to optimize a design by solving quadratic equations, and how increasing the scale of a prototype affects the design parameters for an increased payload.
Unit 3 - Quadratics in The Garden - Designing A Fountain
Students will design a water fountain by writing multiple quadratic equations and graphing them to represent decorative parabolic streams of water. Students will write and graph quadratic equations in both Vertex and Standard Form. The various streams of water will originate from different heights and have different trajectories, requiring students to work in both the first and second quadrants of the cartesian coordinate system. Students must calculate the x and y coordinates of each apex, and each starting and ending point of the stream of water, along with its axis of symmetry, to ensure a decorative and aesthetically pleasing fountain. Once the design is completed, the students must calculate which types of pumps they will need to purchase for each stream of water by analyzing the required pressure and orifice size to ensure the required velocity to ensure the streams follow their designed trajectory.
Unit 3 - Key Assignments
Assignment 1: Graphing Parabolas through x-intercepts:
Students graph quadratics by graphing the x-intercepts first after factoring a simple quadratic equation that fits their first stream of water for the fountain. Students must identify and draw the axis of symmetry by finding the midpoint of the x-intercepts and then locate the vertex of the parabola that will be the stream of water’s trajectory. This method allows students to make connections between the x-intercepts and the parabola. Students draw a sketch of the parabola along with all calculations into their Engineering Notebooks to clarify that the x-intercepts determine the beginning and ending points of each stream of water. Students will also label the x and y coordinates of the vertex, and explain in a short summary how they located each key point of the parabola and describe its significance. Finally, students will plot their equations using an electronic graphing tool (Desmos, Plotly, graphing calculator), verify whether or not their handwritten graphs are accurate, and cite any domain and range restrictions for their designed fountains.
Assignment 2: Graphing through vertex form:
Students will now write equations for two more streams of water in the fountain, but they will find the key points from different information and through a different method of mathematical analysis. Students will be given the apex of two opposing (but symmetrical) streams of water, and must use the vertex form of quadratic equations to find the x-intercepts. Once the quadratic equation that describes the parabolic trajectory is written, students will then convert it from Vertex Form to Standard Form.
This will allow students make connections between the vertex and the parabola. Students will accurately draw each parabola, write the equation in both forms, and describe in their engineering notebooks how to use both Vertex Form and how to convert it to Standard Form for parabolas. Students will also write a short summary of how to precisely determine the apex and x-intercepts, and what the significance of each point is for each stream of water.
Assignment 3: Exploring the leading coefficient:
Students will use online graphing software to explore and understand the impact of various leading coefficients by graphing different quadratic equations in different forms. At first, students will be given x-intercepts, and must write the equation in standard form, then adjust the height of the parabola by adjusting the leading coefficient (scalar multiple). Second, when given the vertex, students will change the leading coefficient to observe the effect on the x-intercepts. Students again will write a summary that explains how the leading coefficient affects the shape of each stream of water. Using this new understanding, students are asked to add two more streams of water that would add to the aesthetic beauty of the existing streams of water (from Assignments 1 and 2). Students must use various “a values”for their new parabolas to show understanding, and must sketch the trajectories in their engineering notebooks along with the appropriate quadratic equations for each new stream of water.
Graphing Software:
- Desmos https://www.desmos.com/
- Plotly https://chrome.google.com/webstore/detail/plotly/khajkhinhblhaenlhpodnblkmpdgclne?hl=en
Math/Lab Assignment 4: Design of Water Fountain
Starting from scratch, students are challenged to create an entirely new water fountain of their own design. Using what they learned from the first three assignments, they must graph and write the equation (in both Standard and Vertex Form) for each stream of water. Students must include appropriate domains and ranges for each equation written. Once the design is complete, the instructor will help students with kinematic equations from physics to find the required velocity to make each fountain precisely match the designed trajectory. Once provided with this velocity, students then research various water pumps by finding the required pressure rating (in psi, or pounds per square inch) for each pump and then identify available pumps from various suppliers (ex. Granger, Ingersoll/Rand, etc.). Students will write a detailed cost proposal that includes specific pump models, specifications, and velocities, and must support their proposal with mathematical evidence justifying the cost of each pump. If budgets allow for it, teachers have the option of actually ordering enough pumps to assemble and test the designed fountains and see if the calculated x-intercepts, apexes, and axes of symmetry match the design.
Extension Assignment - CAD Design of Water Fountain
Using a freely available CAD software program like Sketch-Up or TinkerCAD, students will design the fountain as a virtual 3D object, using the previous calculations to specify the dimensions of the design.
SketchUp(Browser Version)
TinkerCAD( Browser-based)
https://www.tinkercad.com/
Unit 4 - Balloon Rockets
Students will follow the engineering design process to design a transport vehicle that will travel an unknown distance powered by an inflated balloon. Built from simple materials, the student-made vehicles will race across the room while suspended from two fishing lines. Students will implement and diagram the Universal Systems Model of problem solving to develop their vehicles. Once built, students will gather test data to explore mathematical relationships and patterns between the balloon’s volume, radius, and distance traveled. Students will plot multiple data points for a wide variety of balloon volumes to develop a graph that will allow them to use the relevant independent variable (balloon size) to predict the value of the dependent variable (distance traveled). Students will then be given a predetermined distance, and must use their established function to inflate their balloon accordingly to make their vehicle precisely travel the target distance.
Unit 4 - Key Assignments
Assignment 1: Problem Definition and Idea Generation
Students first draw up plans for their prototypes, which must be approved before getting the materials. Students will create thumbnail sketches, a rough sketch, and a final scaled drawing using measurement of inches. All sketches, drawings, and design notes will be done in students’ engineering notebooks.
Lab Assignment 2: Build The Design
Students will build their design using household materials (paper towel rolls, straws, string, toothpicks, cardboard, etc.). Each student will get a balloon of the same size and color. Students are to build their prototype to carry an object of their choice (lego figurine, washer, weight, etc.). The object must be able to be set on the vehicle without being attached in any way. Students will be given an initial minimum distance their vehicle must travel, as well as a maximum balloon diameter. Students continue to use their engineering notebooks to record data, sketches and such.
Lab Assignment 3: Test and Collect and Analyze
Students will use the mathematical model to figure out a predictable output for their balloon transport vehicle. Using the data, students determine what relationship there is between the variables and write a function equation using proper function notation. They will retest their designs by changing fuel input (balloon inflation) and corresponding mass of vehicle until they find a formula that will allow them to plot data points to accurately predict an outcome. Students will document their design drawings, their test results, and their reflections on the process into their engineering notebooks to record the relationship between balloon volume and distance traveled. On test day they should be able to use their data points based on previous investigation, that will allow them to know how much fuel they will need to reach the unknown distance.
Lab Assignment 4: Enrichment Activity-Optimize Fuel Usage
Performance information will be shared and the students will analyze possible patterns in the data. Students will incorporate the analysis into the redesign process for subsequent redesigns of their vehicles. After students reach the unknown distance on test day, they now must reach that distance using the least amount of fuel as possible. They must optimize fuel usage to determine the most efficient balloon transport vehicle. They will redesign and test to see if mathematical analysis improved their projects.
Unit 5 - Build A Better Bottle
In this unit, students will investigate the behavior of exponential functions while designing a product whose behavior models exponential decay through heat loss. Students will employ the engineering design process to conceive and create an insulated coffee cup/bottle that is constrained by several inputs: size, material costs, safety, and thermal properties. The project begins by defining the needs of the customer and the appropriate design parameters and limitations. Students will then research Newton’s Law of Cooling to better understand how an exponential decay function describes the performance of any device that is designed to retain heat.
Students will then explore the container’s behavior by altering different initial conditions and then using temperature sensors to gather and record data for multiple trials. By graphing this data, students will develop the shape of the cooling curve, and will use graphing tools to match the mathematical function (exponential) to their data. Students then engage in the design process to investigate problem parameters by researching material thermal resistances and material costs. Students create initial design drafts and calculate the material costs for constructing their product.
They then either use a CAD program (or traditional drafting techniques) to finalize their designs, while also calculating the thermal transfer parameters of their design. The students can then use these input parameters in the exponential model to determine the cooling rate for different liquids at different initial temperatures. Finally students create a proposal that includes the efficiency of their design as well as the calculated material cost. These proposals are presented as ideas to a “product manager” who assesses the manufacturability, cost and performance of the proposed products.
AutoDesk Fusion 360( PC/Mac)
http://www.autodesk.com/products/fusion-360/students-teachers-educators
http://www.autodesk.com/products/fusion-360/learn-training-tutorials
Unit 5 - Key Assignments
Lab Assignment 1:Measure cooling rates: Students use temperature sensors or thermometers to measure the cooling rates of a fluid of fixed volume in a coffee cup/water bottle. Students graph the data and then use a graph matching tool (LoggerPro, Excel, Plotly, etc.) to deduce the appropriate type of mathematical function. After sharing data with the entire class, students discuss the similarities and differences between quadratic functions and the behavior of the cooling function. Exponential functions are then introduced with the basic exponential function ( y = ax ), and students are given multiple examples of both growth and decay, along with numerous applications where these situations apply to physical phenomena.
Students are then given the specific mathematical structure of the cooling function:
T (t) = Ae−kt + TA
where TA= ambient temperature in the room, T(t)= temperature of liquid, A= initial temprature difference, k= cooling constant
Students analyze how the different coefficients (A, TA, -k) change the position and curvature of the exponential function. Other exponentia ls are also investigated in order to establish a common pattern. The goal of this assignment is to help guide the students towards an analytical tool for determining a performance function for their product.
Students record data gathered and discussion notes in their engineering notebooks in preparation for the culminating assignment.
Lab Assignment 2: Research Thermal Resistance and Thermal Qualities of Materials
Students research the physical parameters that actually affect the cooling function. This leads then to a discussion and further research into thermal properties of materials. Further investigations are designed to strengthen student understanding of how surface area, thermal resistivity, and thickness change the curvature of the cooling function. Student groups investigate the cooling rate of a known liquid through different containers with different surface areas, different thicknesses and different materials. Students will collectively produce a data report and analysis of the experimental input’s effect on cooling.
Lab Assignment 3: Design A Better Liquid Holder
Students are now given the design challenge parameters for designing a better liquid holder. The design requirements outline specific design parameters such as the size specifications of the product (must fit in a standard size cup holder), the function of the container (must have removeable lid and handle), and the cost range of the product. To better understand the consumer sales perspective of designing products, student designers will survey other students to get customer input on size, shape, and feel of various beverage containers. Once designers have enough responses to ensure statistical significance, they must then compile the data using a scatter plot or other graphical display to demonstrate understanding of customer preferences, so that any functionally-driven design decisions also consider the marketability of the product.
Students then produce design drawings of their product, including material choice and construction design. Once their designs are completed, students must justify the design parameters using mathematical evidence from their explorations of Newton’s Law of Cooling equation. All reflections, calculations, and design sketches are all entered in their engineering notebooks.
Extension Assignment: Model and Predict Product Performance
Using a software thermal analysis tool (Fusion360, etc), students can model the performance of their product based on the design they have proposed. Students generate a thermal analysis report and performance prediction based on material cost and design specs.
AutoDesk Fusion 360( PC/Mac)
http://www.autodesk.com/products/fusion-360/students-teachers-educators
http://www.autodesk.com/products/fusion-360/learn-training-tutorials
OnShape( Browser-based)
https://www.onshape.com/
OPTIONAL
Unit 6 - Design a “FUNctional” Graphical User Interface App
To provide students with an opportunity to use and apply their learning from the year in a new engineering context, students review the functional models covered throughout the course by designing and writing the code for graphical user interfaces, (“apps”) that simulate calculators for each of the mathematical representations or engineering equations covered in the course. The calculator accepts user input for the functional parameters of the problem, and generates the output for each functional model. By writing the computer code that processes the inputs to deliver the correct output, students must thoroughly understand the equations, possible inputs (including appropriate domains for independent variables), and must verify the outputs are flawlessly correct.
Unit 6 - Key Assignments
Assignment 1:
Students have been hired to design a calculator app which simulates different mathematical functions related to the engineering principles studied in the course. Students identify the parameters that each method definition should accept from the user by reviewing the parameters found in each of the three functional representations, and should define what each parameter will represent for the real-world model. The teacher should check that students generate the following functions and parameters:
- Linear: Parameters will likely be the slope (or rate) and y-intercept (starting value). A variation to this might be a linear equation in point-slope form with the slope as one parameter and the x and y coordinates of a data point as the other parameters to the method written.
- Quadratic: Parameters will likely be the a, b, and c values (determined by user input). A typical representation for this might include the equation for projectile motion, with ‘a’ equal to the gravitational constant and the velocity (b) and starting height(c) of the projectile determined by user input.
- Exponential: a and b values determined by the user. One example might include the cooling function studied in the previous unit, with (A, TA, -k) as the coefficients entered by the user.
For each of the three models or apps, students create a “Know/Need to Know” list for the app, which will inform their design decisions. Students write a formal proposal for each app they will design, and a timeline for the project.
Assignment 2: Design GUI: Once students have written the “interface” for the apps, they design each graphical screen which the user will interact with. Students define the screen or frame size according to their desired platform (Android, iPhone, website, etc.) and the typical “consumer” who will use each application, by researching and collecting data on their consumers, and using that data to inform the design decisions they make for the overall layout, colors, text fields, and buttons on the screen.
Students create a Google Form and/or survey for their target audience, with directed questions that will inform the design decisions for the graphical components on their app. Based on their ideal “consumer,” students must determine the questions and information needed for adequate feedback and informed decisions, and must then market the survey to the typical “consumer” within their community.
After gathering market data, students design and color their screen on graph paper, or using a computer application, then present a design proposal to the class for evaluation. After reaching a final design decision, students must identify the x and y coordinates, and dimensions needed, to properly place each component, then write the code for generating the graphical design.
Course Materials
Algebra Textbook: (use approved district math book)
Supplementary Text: Design Engineering Textbook (district approved)